Detect Toeplitz Matrix: Easy Python Guide & Examples

Is your matrix a Toeplitz? Don't worry! This guide breaks down the Toeplitz matrix concept with Python examples, offering simple methods to determine if your matrix follows the diagonal-constant rule. Master this matrix property for coding interviews and data analysis!

What's a Toeplitz Matrix? (And Why Should You Care?)

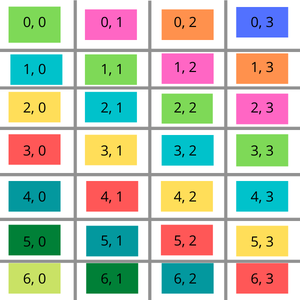
A Toeplitz matrix, also known as a diagonal-constant matrix, has the same elements along each descending diagonal. This means that matrix[i][j] == matrix[i-1][j-1] for all elements within the matrix. Recognizing this pattern is useful in many domains, including:

• Signal Processing: Toeplitz matrices are crucial in analyzing linear time-invariant systems.
• Image Processing: Used in convolution operations and filter design.
• Data Compression: Employed in techniques like the Levinson-Durbin algorithm.

Let's explore how to identify them efficiently!

Method 1: Direct Diagonal Comparison (Simple but Effective)

This approach directly compares each element to the start of its diagonal.

Time Complexity: O(n*m) Space Complexity: O(1)

Here's how it works:

• Iterate through the first row and first column as starting points for diagonals.
• For each diagonal, compare all elements to the starting element.
• If any element doesn't match, it's not a Toeplitz matrix!

def check_diagonal(matrix, row, col):
    n = len(matrix)
    m = len(matrix[0])
    value = matrix[row][col]
    i = row + 1
    j = col + 1

    while i < n and j < m:
        if matrix[i][j] != value:
            return False
        i += 1
        j += 1
    return True

def is_toeplitz_matrix(matrix):
    n = len(matrix)
    m = len(matrix[0])

    for i in range(m):
        if not check_diagonal(matrix, 0, i):
            return False
    for i in range(n):
        if not check_diagonal(matrix, i, 0):
            return False
    return True

# Example usage:
matrix1 = [[6, 7, 8], [4, 6, 7], [1, 4, 6]]
matrix2 = [[6, 3, 8], [4, 9, 7], [1, 4, 6]]

print(f"Matrix 1 is Toeplitz: {is_toeplitz_matrix(matrix1)}")
print(f"Matrix 2 is Toeplitz: {is_toeplitz_matrix(matrix2)}")

Method 2: Compare with the Top-Left Neighbor (Elegant and Concise)

This method simplifies the check by comparing each element with its top-left neighbor. Less verbose, more readable!

Time Complexity: O(n*m) Space Complexity: O(1)

Steps:

• Start from the second row and second column.
• Compare each element with matrix[i-1][j-1].
• If there's a mismatch, the matrix is not Toeplitz.

def is_toeplitz_matrix_optimized(matrix):
    n = len(matrix)
    m = len(matrix[0])

    for i in range(1, n):
        for j in range(1, m):
            if matrix[i][j] != matrix[i - 1][j - 1]:
                return False
    return True

# Example usage:
matrix1 = [[6, 7, 8], [4, 6, 7], [1, 4, 6]]
matrix2 = [[6, 3, 8], [4, 9, 7], [1, 4, 6]]

print(f"Matrix 1 (Optimized) is Toeplitz: {is_toeplitz_matrix_optimized(matrix1)}")
print(f"Matrix 2 (Optimized) is Toeplitz: {is_toeplitz_matrix_optimized(matrix2)}")

Method 3: Using Hashing to Identify Diagonals (Advanced Approach)

This approach uses a hash map to store the first element of each diagonal.

Time Complexity: O(n*m) Space Complexity: O(number of diagonals) or O(m+n)

Steps:

1. Calculate the "diagonal key" (row index - column index) for each element.
2. Store the first encountered element for each key in a hash map.
3. If a subsequent element on the same diagonal doesn't match the stored value, return False.

def is_toeplitz_matrix_hashing(matrix):
  mp = {}
  for i in range(len(matrix)):
    for j in range(len(matrix[0])):
      key = i - j
      if key not in mp:
        mp[key] = matrix[i][j]
      elif mp[key] != matrix[i][j]:
        return False
  return True

# Example usage:
matrix1 = [[6, 7, 8], [4, 6, 7], [1, 4, 6]]
matrix2 = [[6, 3, 8], [4, 9, 7], [1, 4, 6]]

print(f"Matrix 1 (Hashing) is Toeplitz: {is_toeplitz_matrix_hashing(matrix1)}")
print(f"Matrix 2 (Hashing) is Toeplitz: {is_toeplitz_matrix_hashing(matrix2)}")

Choosing the Best Method

• For simplicity and readability, the optimized comparison method (Method 2) is generally preferred.
• If space complexity is a major concern and you are working with extremely large matrices Direct Diagonal Comparison (Method 1) provides o(1) space complexity.
• The hashing method is useful for understanding diagonal properties, but its higher space complexity makes it less practical unless you are working on a distributed architecture.

Now you're equipped to conquer Toeplitz matrices! Use these methods to efficiently identify and utilize this special matrix structure in your projects.