Maîtrisez l'Algorithme de Warnsdorff : Le Guide Ultime pour Résoudre le Problème du Cavalier aux Échecs

Vous cherchez une solution élégante au casse-tête du parcours du cavalier aux échecs ? Découvrez l'algorithme de Warnsdorff, une méthode simple et efficace pour visiter chaque case de l'échiquier une seule fois. Ce guide vous explique tout !

Qu'est-ce que l'Algorithme de Warnsdorff et Pourquoi l'Utiliser ?

L'algorithme de Warnsdorff est une heuristique puissante pour résoudre le problème du parcours du cavalier. Son atout majeur ? Il est beaucoup plus rapide et nécessite moins de "backtracking" que les approches naïves.

• Simplicité: Facile à comprendre et à implémenter.
• Efficacité: Trouve une solution rapidement dans la plupart des cas.
• Visualisation: Permet de visualiser un parcours complet du cavalier.

Les Bases : Comprendre le Problème du Cavalier

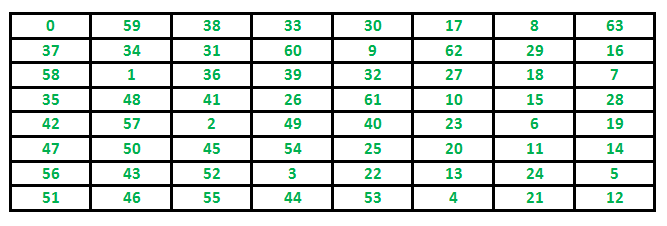
Le problème du parcours du cavalier consiste à trouver une séquence de mouvements pour un cavalier d'échecs de manière à ce qu'il visite chaque case d'un échiquier une seule fois.

• Départ: Le cavalier commence sur une case vide.
• Mouvement: Le cavalier se déplace selon ses règles traditionnelles (en L).
• Objectif: Visiter chaque case exactement une fois.

Comment l'Algorithme de Warnsdorff Simplifie le Problème

L'algorithme de Warnsdorff repose sur une règle simple : minimiser l'accessibilité. Autrement dit, à chaque mouvement, le cavalier choisit la case adjacente non visitée qui a le moins d'autres cases non visitées accessibles.

• Moins d'Impasses: Réduit les chances d'atteindre une case sans issue.
• Choix Stratégiques: Force le cavalier à explorer les zones les plus "restreintes" en premier.
• Solution Optimale: Augmente significativement les chances de trouver un parcours complet.

Étape par Étape : Application Pratique de l'Algorithme

Suivez ces étapes simples pour implémenter l'algorithme de Warnsdorff:

1. Initialisation: Choisissez une case de départ aléatoire. Marquez-la comme visitée.
2. Calcul d'Accessibilité: Pour chaque case adjacente non visitée, calculez son "degré" (nombre de cases non visitées accessibles depuis cette case).
3. Mouvement Optimal: Déplacez le cavalier vers la case adjacente avec le degré minimal.
4. Répétition: Répétez les étapes 2 et 3 jusqu'à ce que toutes les cases soient visitées ou qu'il n'y ait plus de mouvements possibles.
5. Vérification: Si toutes les cases sont visitées, vous avez trouvé un parcours du cavalier. Sinon, recommencez à l'étape 1.

Code en C++ : Une Implémentation Concrète

Le code C++ fourni illustre l'implémentation de l'algorithme de Warnsdorff. Il calcule le degré de chaque case adjacente et choisit le mouvement optimal. Analyser ce code vous donnera une compréhension plus approfondie de l'algorithme.

// C++ program to for Knight's tour problem using
// Warnsdorff's algorithm
#include <iostream>
#define N 8

// ... (Le reste du code C++ se trouve dans le contenu original) ...

Note : Le code Java fourni fonctionne de la même manière.

Astuces et Pièges à Éviter pour un Parcours Réussi

Voici quelques conseils pour maximiser vos chances de succès:

• Départ Stratégique: Commencer près du centre peut augmenter les chances de succès.
• Gestion des Impasses: Si l'algorithme bloque, redémarrez à partir d'une autre case.
• Optimisation: Expérimentez avec différentes stratégies de départ et d'exploration.

Prochaines Étapes : Défis et Applications Avancées

Une fois que vous maîtrisez l'algorithme de Warnsdorff sur un échiquier standard, essayez ces défis:

• Tailles d'Échiquier Variables: Adaptez l'algorithme à des échiquiers de différentes tailles.
• Parcours Fermés: Recherchez des parcours où le cavalier peut revenir à sa case de départ.
• Autres Graphes : Appliquez l'algorithme de Warnsdorff à d'autres problèmes de parcours de graphes.

En conclusion, l'algorithme de Warnsdorff est un outil précieux pour résoudre le problème du parcours du cavalier. Sa simplicité et son efficacité en font un excellent point de départ pour explorer les algorithmes de backtracking et les problèmes de parcours de graphes.