Détecter une Matrice de Toeplitz : 3 Méthodes Simples et Efficaces

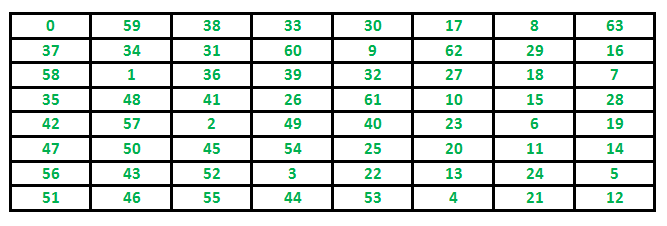
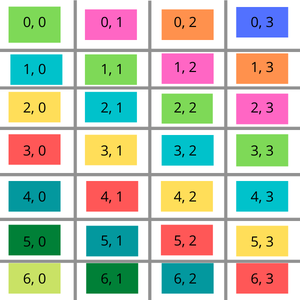
Vous vous demandez si une matrice est de Toeplitz ? Ce type particulier de matrice, où les diagonales descendantes ont toutes les mêmes valeurs, se retrouve dans divers domaines, de la science des données au traitement du signal. Découvrez comment l'identifier rapidement grâce à ces 3 approches testées et approuvées pour une détection précise.

1. Vérification Diagonale Complète : La Méthode Infaillible (O(n*n))

Cette méthode consiste à examiner chaque diagonale descendante en utilisant les éléments de la première ligne et de la première colonne comme point de départ. Elle garantit une couverture exhaustive et une identification précise des matrices de Toeplitz.

• Comment ça marche ? Pour chaque diagonale, on compare chaque élément avec la valeur d'origine.
• Quand l'utiliser ? Idéal pour les matrices de toutes tailles, en particulier lorsque la simplicité et la certitude sont privilégiées.
• Pourquoi c'est efficace ? Chaque élément est vérifié par rapport à sa diagonale, éliminant ainsi toute possibilité de faux positif.

2. Comparaison Diagonale Rapide : L'Approche Optimisée pour la Performance (O(n*n))

Ici, on compare chaque élément à son voisin en haut à gauche. Cette technique est optimisée pour la vitesse et minimise le nombre de comparaison nécessaires.

• Comment ça marche ? On parcourt la matrice à partir de la deuxième ligne et de la deuxième colonne, comparant chaque élément mat[i][j] avec mat[i-1][j-1].
• Quand l'utiliser ? Parfait pour les grandes matrices où l'efficacité est essentielle.
• Pourquoi c'est efficace ? Elle s'arrête immédiatement si une divergence est détectée, évitant ainsi les comparaisons inutiles.

3. Hachage Ingénieux : Une Solution Économique en Espace (O(n*n) Temps, O(n) Espace)

Cette approche utilise une table de hachage pour stocker la première valeur rencontrée pour chaque diagonale et vérifie ensuite que les éléments suivants correspondent. Cela exploite l'espace mémoire pour optimiser la détection.

• Comment ça marche ? On calcule une clé unique pour chaque diagonale (la différence entre l'indice de ligne et l'indice de colonne) et on la stocke dans une table de hachage.
• Quand l'utiliser ? Utile lorsque l'espace est limité mais qu'une identification rapide est requise.
• Pourquoi c'est efficace ? La table de hachage permet un accès rapide aux valeurs diagonales, réduisant ainsi le temps de recherche.

Comprendre ces trois méthodes vous permet de choisir l'approche la plus adaptée à vos besoins spécifiques. Que vous privilégiez la simplicité, la vitesse ou l'optimisation de l'espace, vous disposez maintenant des outils pour détecter une matrice de Toeplitz avec précision et efficacité.