Comment vérifier efficacement si une matrice est une matrice de Toeplitz : Guide simple et rapide

Les matrices de Toeplitz, également appelées matrices à diagonale constante, sont des structures mathématiques spécifiques qui présentent des propriétés intéressantes. Cet article vous guide à travers des méthodes simples et efficaces pour déterminer si une matrice donnée est une matrice de Toeplitz.

Qu'est-ce qu'une matrice de Toeplitz et pourquoi devriez-vous vous en soucier ?

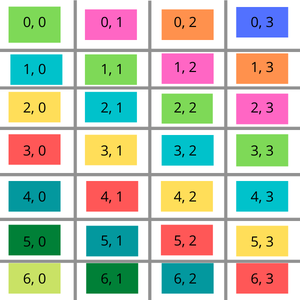
Une matrice de Toeplitz se caractérise par le fait que chaque diagonale descendante de gauche à droite possède des éléments identiques. En termes plus simples, pour tout élément mat[i][j], sa valeur doit être la même que celle de mat[i-1][j-1]. Comprendre et identifier ces matrices est crucial dans de nombreux domaines comme le traitement du signal, l'analyse d'images et la résolution de systèmes linéaires.

Méthode 1 : Vérification de chaque diagonale – Complexité temporelle O(n * n) et complexité spatiale O(1)

Cette méthode consiste à parcourir chaque diagonale descendante de la matrice en utilisant chaque élément de la première ligne et chaque élément de la première colonne comme point de départ. On vérifie ensuite que chaque élément le long de cette diagonale correspond à la valeur de son point de départ.

Comment ça marche ?

1. Définir n = mat.size() et m = mat[0].size().
2. Pour chaque index de colonne i de 0 à m - 1, appeler checkDiagonal(mat, 0, i). Si la fonction renvoie false, retourner immédiatement false de isToeplitz.
3. Pour chaque index de ligne i de 0 à n - 1, appeler checkDiagonal(mat, i, 0). Si la fonction renvoie false, retourner immédiatement false de isToeplitz.
4. Si tous les appels à checkDiagonal réussissent, retourner true.

Cette approche assure une vérification complète et est simple à mettre en œuvre.

Méthode 2 : Vérification de l’élément diagonalement supérieur – Complexité temporelle O(n * n) et complexité spatiale O(1)

Cette approche plus efficace consiste à scanner chaque cellule à partir de la deuxième ligne et de la deuxième colonne en comparant chaque valeur à son voisin en haut à gauche.

Pourquoi cette méthode est-elle rapide ?

• Efficacité : Une fois qu’une correspondance incorrecte est détectée, elle s’arrête immédiatement.
• Simple : Facile à comprendre et à mettre en œuvre.

Étapes à suivre :

1. Définir n = mat.size() et m = mat[0].size().
2. Itérer i de 1 à n - 1 et dans cette itération j de 1 à m - 1.
3. Si mat[i][j] != mat[i - 1][j - 1] à un certain point, retourner false.
4. Une fois que toutes les paires ont été vérifiées sans aucune correspondance incorrecte, retourner true.

Méthode 3 : Utilisation du hachage – Complexité temporelle O(n * n) et complexité spatiale O(n)

Cette méthode attribue un identificateur unique à chaque diagonale descendante (l'index de ligne moins l'index de colonne) et utilise une Table de hachage pour enregistrer la première valeur observée pour cette diagonale.

Comment le hachage peut-il vous aider ?

• Identification unique : Une valeur unique est créée pour chaque diagonale.
• Stockage efficace : Permet une recherche rapide pour détecter les incompatibilités.

Procédure :

1. Déterminer les dimensions de la matrice (nombre de lignes et nombre de colonnes) à partir de mat.
2. Créer une Table de hachage vide mp pour mapper chaque clé diagonale à sa valeur représentative.
3. Parcourir chaque cellule de mat par son index de ligne i et son index de colonne j.
4. Pour chaque cellule, former la clé diagonale en soustrayant j de i.
5. Si mp contient déjà cette clé, comparer l'élément actuel à la valeur stockée ; s'ils sont différents, retourner false immédiatement.
6. Si la clé n'est pas encore dans mp, enregistrer l'élément actuel sous cette clé.
7. Si le parcours est terminé sans aucune correspondance incorrecte, retourner true.

En adoptant cette méthode, vous pouvez identifier efficacement les matrices de Toeplitz en utilisant l'efficacité des Tables de hachage.