Toeplitz行列かどうかを効率的に判定する方法：3つのアプローチ

Toeplitz行列（または対角一定行列）とは、左から右へ向かう各下降対角線の要素がすべて同じ値である行列のことです。与えられた正方行列がToeplitz行列であるかどうかを判定する効率的な方法を3つご紹介します。

アプローチ1：各対角線をチェック - O(n * n) 時間、O(1) 空間

このアプローチでは、行列の最初の行と最初の列の各要素を出発点として、すべての右下方向の対角線を走査します。各対角線上のすべての要素が、その対角線の先頭要素と一致することを確認します。

• メリット：空間効率が高い（O(1)）。
• デメリット：すべての対角線をチェックするため、計算コストが高い（O(n * n)）。

手順:

1. n = mat.size()、m = mat[0].size()とします。
2. 列インデックスiを0からm - 1まで繰り返します。
   • checkDiagonal(mat, 0, i)を呼び出し、falseが返されたらすぐにfalseを返します。
3. 行インデックスiを0からn - 1まで繰り返します。
   • checkDiagonal(mat, i, 0)を呼び出し、falseが返されたらすぐにfalseを返します。
4. すべてのcheckDiagonalの呼び出しが成功したら、trueを返します。
5. checkDiagonal(mat, x, y)では、i = x+1、j = y+1に対してmat[i][j]をmat[x][y]と比較し、i < n && j < mの間繰り返します。最初に不一致が発生した場合はfalseを返し、エッジに到達した場合はtrueを返します。

アプローチ2：対角線上の要素をチェック - O(n * n) 時間、O(1) 空間

2行目と2列目以降のすべてのセルをスキャンし、各値を左上の隣接要素と比較します。一致しない要素が見つかった場合は、すぐにfalseを返し、最後まで不一致がなければtrueを返します。

• メリット：実装が比較的簡単で、空間効率が高い（O(1)）。
• デメリット：こちらも計算コストが高い（O(n * n)）。

手順:

1. n = mat.size()、m = mat[0].size()とします。
2. iを1からn - 1まで、その中でjを1からm - 1まで繰り返します。
3. mat[i][j] != mat[i - 1][j - 1]が一つでもあれば、falseを返します。
4. すべてのペアをチェックし、不一致がなければ、trueを返します。

アプローチ3：ハッシュを使用 - O(n * n) 時間、O(n) 空間

各右下対角線に一意の識別子（行インデックスから列インデックスを引いた値）を割り当て、その対角線で最初に見られた値をハッシュマップに記録します。行列全体をスキャンし、各セルに対してこのキーを計算し、格納されている値と一致するかどうかを確認するか、新しい場合は格納します。不一致が見つかった場合はすぐにfalseを返し、そうでない場合は最後にtrueを返します。

• メリット：概念的に理解しやすい。
• デメリット：追加の空間（O(n)）を使用し、ハッシュ計算のオーバーヘッドがある。

手順:

1. 行列の次元（行数と列数）をmatから決定します。
2. 各対角線キーをその代表値にマッピングするための空のハッシュマップmpを作成します。
3. 行インデックスiと列インデックスjでmatのすべてのセルを走査します。
4. 各セルについて、iからjを引いて対角線キーを作成します。
5. mpが既にこのキーを持っている場合は、現在の要素を格納されている値と比較します。異なる場合は、すぐにfalseを返します。
6. キーがまだmpにない場合は、そのキーの下に現在の要素を記録します。
7. 不一致なしにトラバーサルを完了した場合は、trueを返します。

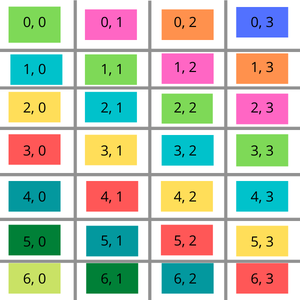
イラスト:

下図は、このアイデアをよりわかりやすく示しています。

黄色で色分けされた対角線を考えてみましょう。この対角線上の任意のインデックスのx値とy値の差は2です（2-0、3-1、4-2、5-3）。同じことが、他のすべての本体対角線についても観察できます。

この３つのアプローチの中から、状況に応じて最適なものを選択してください。一般的には、空間効率を重視する場合はアプローチ1または2が適しており、より直感的な理解を求める場合はアプローチ3が適しています。