Toeplitz行列判定：効率的なアルゴリズム3選 - シンプルな解説と実装

Toeplitz行列という言葉を聞いたことがありますか？ 簡単に言うと、左上から右下へ向かう対角線上の要素がすべて同じ値を持つ行列のことです。この記事では、与えられた行列がToeplitz行列であるかどうかを判定する効率的なアルゴリズムを3つ紹介します。

1. 各対角線をチェックする方法（O(n * n) 時間, O(1) 空間）

このアプローチは、すべての対角線に対して、その要素がすべて同じ値を持つかどうかを検証します。

• 考え方: 行列の最初の行と最初の列の各要素を始点として、各対角線をたどります。
• 手順:
  • n = 行列の行数、m = 行列の列数とします。
  • 最初の行の各列インデックス i (0 から m - 1) について、checkDiagonal(mat, 0, i) を呼び出します。もし false が返される場合、すぐに false を返します。
  • 最初の列の各行インデックス i (0 から n - 1) について、checkDiagonal(mat, i, 0) を呼び出します。もし false が返される場合、すぐに false を返します。
  • すべての checkDiagonal の呼び出しが成功した場合、true を返します。
  • checkDiagonal(mat, x, y) では、i = x + 1, j = y + 1 に対して mat[i][j] を mat[x][y] と比較します。i < n && j < m の間、不一致があれば false を返し、そうでなければ端に達するまで true を返します。

2. 対角線上の要素をチェックする方法（O(n * n) 時間, O(1) 空間）

よりシンプルなアプローチとして、すべての要素をその左上の隣の要素と比較します。

• 考え方: 2行目、2列目以降の各セルをスキャンし、それぞれの値を左上にある隣の値と比較します。
• 手順:
  • n = mat.size()、m = mat[0].size() とします。
  • i を 1 から n - 1 まで、その内側で j を 1 から m - 1 まで反復処理します。
  • もし mat[i][j] != mat[i - 1][j - 1] であれば、false を返します。
  • 不一致なしにすべてのペアがチェックされたら、true を返します。

3. ハッシュテーブルを使う方法 (O(n * n) 時間, O(n) 空間)

このアルゴリズムは、ハッシュテーブルを使用して、各対角線に関連付けられた値を格納します。

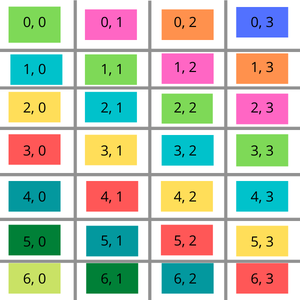
• 考え方: 右下方向の各対角線に一意の識別子（行インデックスから列インデックスを引いたもの）を割り当て、ハッシュマップを使用して、その対角線で最初に見られた値を記録します。
• 手順:
  • 行列のサイズ（行数と列数）を mat から決定します。
  • 各対角線のキーをその代表的な値にマッピングするための空のハッシュマップ mp を作成します。
  • mat 内のすべてのセルを、その行インデックス i と列インデックス j でウォークスルーします。
  • 各セルに対して、i から j を引いて対角線のキーを形成します。
  • もし mp がすでにこのキーを保持している場合、現在の要素を格納されている値と比較します: 値が異なる場合はすぐに false を返します。
  • キーがまだ mp にない場合、現在の要素をそのキーの下に記録します。
  • 不一致なしにトラバーサルを完了した場合、true を返します。

ハッシュテーブルを使用すると、最初のアプローチや2番目のアプローチよりもわずかに複雑になります。しかし、理解を助けるために、以下のような図を参考にしてください。

これらのアルゴリズムを使用することで、与えられた行列がToeplitz行列であるかどうかを効率的に判定できます。選択するアルゴリズムは、空間計算量と時間計算量のトレードオフによって異なります。ほとんどの場合、最初の2つのアルゴリズムがシンプルで効率的です。